What can Dwight teach us about the signs of products/quotients?
A positive times a positive is a positive
A negative times a positive is a negative
A positive times a negative is a negative
A negative times a negative is a positive.
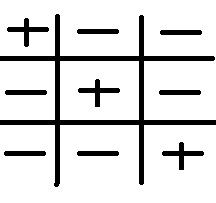
You've probably even used the little tic-tac-toe chart to remember.
Think of the positive sign as love and think of the negative sign as hate.
If someone loves to love that's a positive thing (So a positive times a positive is a positive)
If someone loves to hate that's a negative thing (So a positive times a negative is a negative)
If someone hates to love that's a negative thing (So a negative times a positive is a negative)
If someone hates to hate that's a positive thing (So a negative times a negative is a positive)
If that one doesn't do it for you try looking at it like this:
A positive sign is a friend and a negative sign is an enemy.
A friend of your friend is your friend (So a positive times a positive is a positive)
A friend of your enemy is your enemy (So a positive times a negative is a negative)
An enemy of your friend is your enemy (So a negative times a positive is a negative)
An enemy of your enemy is your friend (So a negative times a negative is a negative)
Just ask Dwight from the office he'll tell you all about it... check out the video below.
Ugh, Factoring, How do I decide which method to use?
Putting an equation in y=mx + b form.
Simplifying Radicals (index=2)
Using the Pythagorean Theorem throughout High School
Factoring Trinomials
Here you will learn how to factor a trinomial by working out an example. Suppose you are asked to factor:
x2 - 14x - 15
First set up two sets of parentheses like this ( ) ( ) Since the first term in the trinomial is the product of the first terms of the binomials, you enter x as the first term of each binomial
(x ) (x )
Now to get the next two terms you need to ask youself: What multiplies to -15 and at the same time adds up to -14?
Well lets answer the first question: -3*5 multiplies to -15 but it adds up to 2. How about -15*1? Yes this will work because it multiples to -15 and -15+1=-14 and so you get:
(x - 15)(x + 1).
To check your answer simply use FOIL to see if it returns to the original equation.
Go to this website for some examples
Then
Go to this website to check your answers.
Solving for the Roots

Above is the quadratic formula. Do not be intimidated, you will find this formula to be very simple. The standard form of a quadratic equation is ax2 + bx + c = 0, where a, b, c, are real numbers and a cannot equal 0. For any quadratic equation in standard form, the solutions can be found by using the quadratic formula
Remember, the quadratic equation must be in standard form before using the quadratic formula. The value of b2 - 4ac in the quadratic formula is called the discriminant If the discriminant is negative, the quadratic formula will yield two complex solutions. If b2 - 4ac = 0, there will be one repeated solution, and if it is positive, there will be two real number solutions.
Now work on the following Problem and solve for x
x^2 + 7x + 6 = 0
Scroll down for the answer.........
Did you get the values of x? Notice I said values and not value, You will always get two answers when using the quadratic formula, However sometimes the values will repeat. Your answer should have been x=-6 and x=-1
Now go to this Website and where it says y1 write in our quadratic equatiion and answer the following questions.
1. At what points does the Parabola intersect with the x-axis?
2. Are the points of intersection the same as the x values we found when using the quadratic formula? Why? Justify your answer.
3. Come up with your own quadratic equation and graph it at the aforementioned website. When you are done analyze your graph. Does it intersect with the x axis? If so how many times?