What's your interpretation of the quote? Add your voice or comments by clicking on the plus sign in the lower middle after hitting play. You will have to create a voice-thread account first. (This is a good way to take into account student voice)

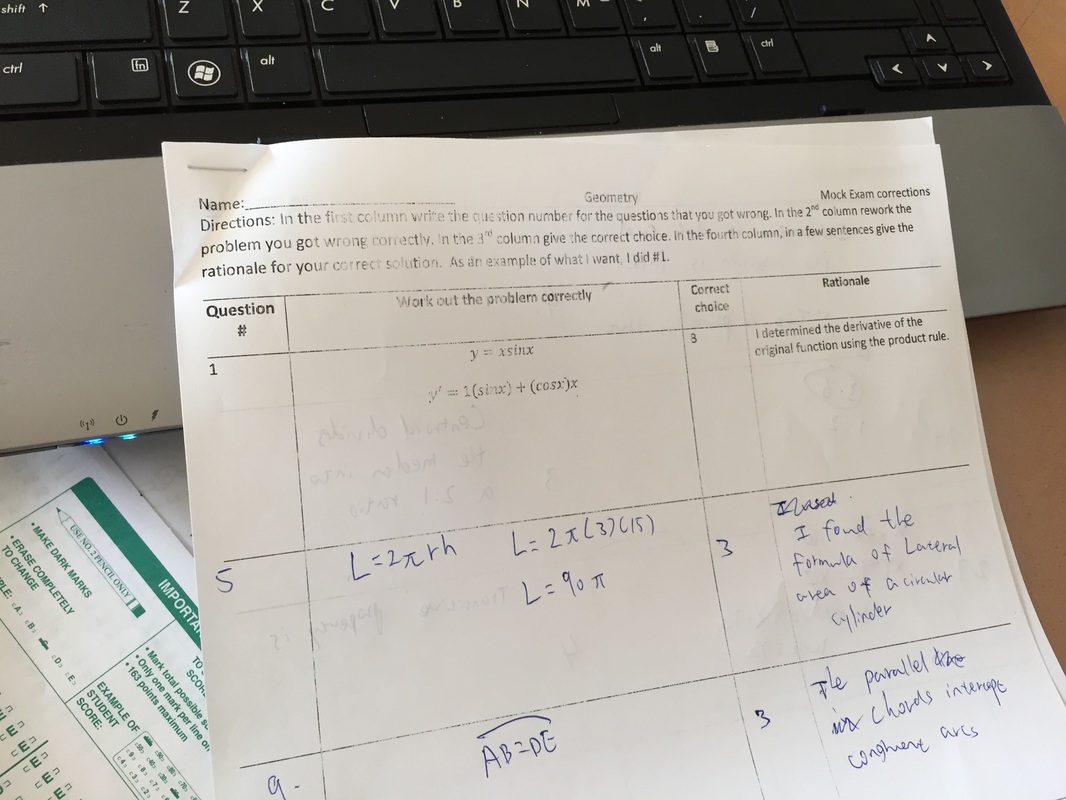
Here is a pic of a student correcting his mock Geometry regents. It was real useful to have the video because students got to cover what they needed. Students can focus on their weaknesses and reflect on their own needs rather than sit and wait for me to get to the problem they need.

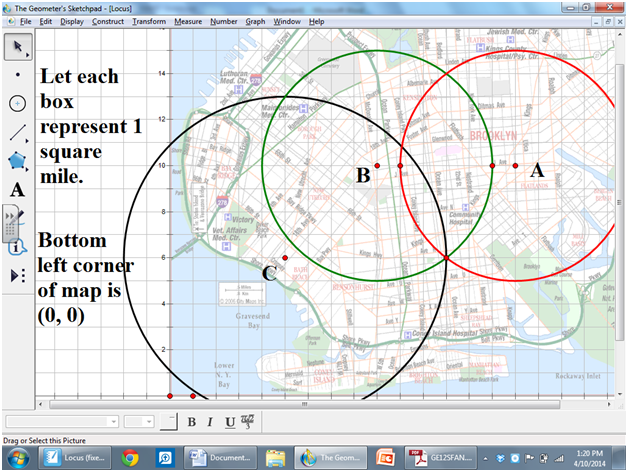
Normally, when I used to introduce locus my aim looked like this:
Aim: How do we sketch the locus of points a fixed distance from a point?

This year it looked like this:
Aim: How do cell phone towers determine the location of a customer?

Huge difference, and you can note the difference in the level of engagement the minute students read the aim walking into the room.

Before the break I found a really awesome lesson at Mathalicious.com. The lesson looked at locus, more specifically focused on the locus of points a fixed distance from a point. They really did a great job putting this lesson together. Below is a pic of a part of the lesson I did with my students.
Essentially the lesson first seeks to answer: How many cell phone towers does it take to determine a customer's location?
Students then go through a series of activities involving locus to determine this.

There are three main parts to the lesson but since I was using it to introduce locus, we just focused on that part of the lesson that looks at how many towers are needed to track a persons location. (Although we will probably later do the rest since the whole lesson is rich).
I tried to make the lesson more personal to my students by using a map of Brooklyn instead of the provided map of Albuquerque. This was easy, just copied and pasted a map of Brooklyn to sketchpad and had students download the pre-arranged file off my website. 

The lesson is a beauty, I really didn't have to change much. Overall, this really is a great lesson with very good questions. The lesson is also universally accessible, all of my students were engaged and I have the observation report to prove it!

With all the new changes now taking place (eg: Common Core) I believe the one that sticks out the most is: Learner-centered environment. It seems to me, that all of these changes seek to create a classroom environment where the student is doing math not watching the teacher do math. So what does a learner centered environment look like in a math class? I think that this is summarized in the 8 standards for mathematical practice:

1.       Make sense of problems and persevere in solving them

2.       Reason abstractly and quantitatively

3.       Construct viable arguments and critique the reasoning of others

4.       Model with mathematics

5.       Use appropriate tools strategically

6.       Attend to precision

7.       Look for and make use of structure

8.       Look for and express regularity in repeated reasoning

If you think about it, all of the above standards are learner-centered. They are all trying to get students to do something, not watch the teacher do something. Here is where the flipped classroom comes in.

The flipped classroom is a model of instruction in which the traditional lecture in class and homework at home model is flipped. Generally, in the flipped classroom students watch lectures at home while the class time is devoted to exercises, projects or discussions.

In a traditional 40 minute lecture setting classroom you have about 15 minutes, tops, of collaborative work amongst students, due to the fact that you’ll spend 15-20 minutes lecturing, 5-10 minutes on a Do now/warm up and 5-10 minutes going over hw. Is it possible to have any of the above standards taking place in 15 minutes? I suppose it is, but in the flip classroom, I believe the time for collaborative work is maximized.

The flip classroom eliminates the lecture time from the classroom by transferring it to the home thereby possibly doubling the time you devote to collaborative work in the class. In my own experience, I have seen the great benefit of devoting more of the chunk of time to collaborative work. It really makes the class a learner-centered environment and allows for things like constructing viable arguments and critiquing the reasoning of others to occur more naturally, rather than trying to speed up the process because you are pressed for time.

Much of the research surrounding the flipped classroom method is fairly new, but here are some statistics from a survey published in a study by Renner, Hamden and McKnight: 100% of educators using the flipped classroom agreed that after flipping their classrooms learning became more active and 80% of students agreed that the flipped classroom allows them to have more constant and positive interactions with their peers and teachers during class time. Also, 70% of the students surveyed agreed that because of the flipped classroom they are more likely to engage in critical thinking and problem solving.

One of the criticisms for the flipped classroom is that it eliminates the face to face time, or takes away the human element. However, flipping the classroom isn’t just about creating videos and having students watch them at home so that the teacher can sit back and watch students do homework in class. It’s about transferring the lecture to the home so that the classroom can be a community of collaborative learners, a place where students are at the very center of learning. It’s about maximizing the time in class where students are doing math not watching the teacher do math. 

You've probably heard it a million times.
A positive times a positive is a positive
A negative times a positive is a negative
A positive times a negative is a negative
A negative times a negative is a positive.

You've probably even used the little tic-tac-toe chart to remember.

Well here is another one to add to your already long list. I got this idea from a friend of mine, Ms.Goebel, Math teacher at Murrow HS.
Think of the positive sign as love and think of the negative sign as hate.

If someone loves to love that's a positive thing (So a positive times a positive is a positive)
If someone loves to hate that's a negative thing (So a positive times a negative is a negative)
If someone hates to love that's a negative thing (So a negative times a positive is a negative)
If someone hates to hate that's a positive thing (So a negative times a negative is a positive)

If that one doesn't do it for you try looking at it like this:
A positive sign is a friend and a negative sign is an enemy.
A friend of your friend is your friend (So a positive times a positive is a positive)
A friend of your enemy is your enemy (So a positive times a negative is a negative)
An enemy of your friend is your enemy (So a negative times a positive is a negative)
An enemy of your enemy is your friend (So a negative times a negative is a negative)

Just ask Dwight from the office he'll tell you all about it... check out the video below.

Today was a pretty awesome day, it was pi day and I got retweeted by Edward Frenkel. The tweet was about a conversation I had with my students about pi and what it represents. What really surprised me was how deep our conversation got. It started when a student asked: Who invented pi? I saw this as a teachable moment and pounced on it.

"Well no one 'invented' pi, really, pi is something that was discovered".

Queu in the article written by Frenkel "Is the universe a simulation?". The thing that stuck out to me about this article was how clearly Frenkel articulated that the truths of Math are necessary and timeless. For example if no one in Greece 2000 years had discovered pi, someone else eventually would.

So that's what I said to my students.

"No one said 'let's make pi 3.14', it's just something that is what it is, someone discovered that it takes approximately 3 diameters and a bit more of one to make the circumference."

This then led to the last part of our conversation: Is pi something that is part of the "code" the Programmer used to create the simulation Frenkel talks about?

Anyways it was a conversation that left us with more questions than answers, but in in a good way, like in an awe and wonder kind of way.

Which leads to my last point. As much as I love pie, sometimes I do feel that this day should be less about pie and more about pi! The math pi. That's exciting in itself. As Brian Lehrer put it "Celebrating pi day with pies would be like celebrating Martin Luther King day with king size candy bars". I mean there really is no connection between pi and pies, unless of course you see the pie as a circle, have kids measure the circumference, measure the diameter, oh wait on second thought hold the pie, maybe there is a connection here.

     Today I was assigned to be a grader at New Utrecht HS for the January 2014 Geometry regents. Last year, I was at Lincoln and had a pleasant experience mingling and exchanging ideas with other teachers. Today was no exception.
     I had the opportunity to exchange with a lead teacher from HS of Telecommunications (Also my alma mater) and it was such a productive today.  She really pointed me to some really useful tools.
     She introduced me to www.deltamath.com which is basically a site that allows math teachers to assign problems to students as hw assignments and does the grading as well. Teachers can also set due dates. They have a great selection of problems in their advanced algebra/trig section that teachers can select from. She also gave me some ideas on how to teach recursive functions and rationals. 

   One of the expectations with the new common core math curriculum is that students will be able to critique each other's reasoning. This is not an easy thing to facilitate for many reasons and not just academic ones. First, the human ego runs away from criticism for fear of being hurt, human pride naturally takes a hit during criticism. Second, people do not know how to give criticism.

   But if we are going to teach kids to be receptive to criticism, I think that the best thing a teacher can do is to create a classroom environment where mistakes are seen as a good thing. Over the summer I took a course with Jo Boaler and she really does a great job of showing why mistakes are not just important but a necessary thing to learn Math. Now I have begun to realize also that creating a culture that is accepting of mistakes creates an environment where students feel motivated to experiment and as Ms. Frizzle would say "Get messy" and not just find right answers.

   So what does creating a culture welcoming of mistakes have to do with criticism? I believe that if your classroom environment is welcoming of mistakes then students would be more open to receiving criticism and giving it.

   Finally, I think that one of the best things a teacher can do to foster this environment is for the teacher himself/herself to be open to criticism. The teacher should not shy away from having students point out different ways of solving a problem or should not become defensive when a student tries to correct him/her (Even if the student is wrong), the teacher should always be open to being questioned and criticized. In conclusion, the best way to teach students to be receptive to criticism is to model it.

In my Advanced Algebra/ Trig class we’ve been doing a unit on statistics. Recently, we covered the topic of dispersion and looked at ways to measure it (Variance and Standard deviation). To make it interesting we looked at Tim Tebow’s rushing stats for that magical year (2011) in which he was the quarterback of the Denver Broncos.

One of the things we found was that there was a huge variance and standard deviation compared to other running backs.

This led to an interesting discussion on which sports exhibit low dispersions when it comes to final scores. The sports mentioned were, soccer and tennis because the scores usually stay consistent. One student had mentioned basketball because the scores are so high but then one student was quick to point out that high scores have nothing to do with dispersion, “It’s about data consistency” he remarked.

This again led to a discussion on Tebow, one student said “You know what’s consistent about him? His terrible passing stats, he consistently sucks at passing and his passing stats show it” One student remarked “Yeah. That would mean his passing stats should have low measures of dispersion. But not in a good way”

Then another student said, “But what about his game against the Steelers?” Someone then pointed out that would be an outlier, something that is considered out of the norm.

In retrospect this was great discussion, throughout the discussion students exhibited a strong grasp of what dispersion is and how data affects the measures of dispersion.