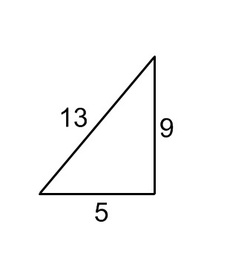
A soup company decides to increase the height of its cans by 30 percent but to keep the volume the same. Approximately how much must the radius of the can be decreased to keep the volume constant?

The triangle to the left is not drawn to scale. The measurements of the lengths of the sides are 13, 9 and 5. Determine if the triangle is a right triangle, justify your response

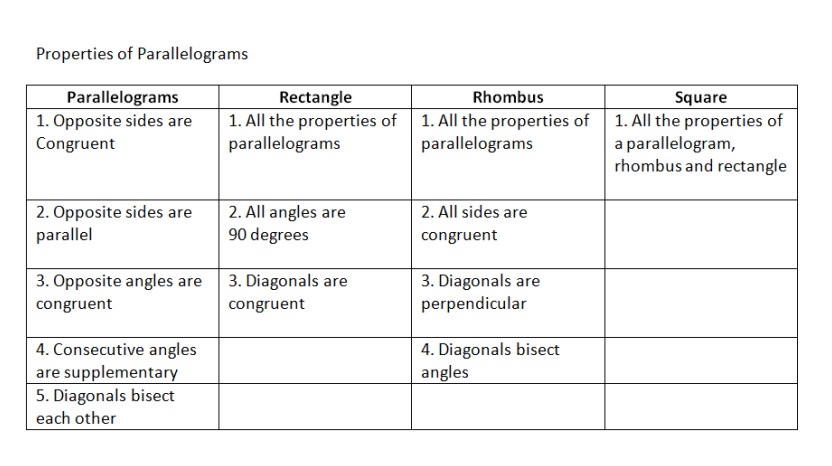
How to prove a quadrilateral is a parallelogram

To prove a quadrilateral is parallelogram, demonstrate that the opposite sides are congruent.  To do this you will need to do the distance formula 4 times. After you are done doing the distance formula 4 times, you can write something like this:

“The quadrilateral is a parallelogram because the opposite sides are congruent”.

How to prove a quadrilateral is a rhombus

To prove a quadrilateral is rhombus you must first prove the quadrilateral is a parallelogram (See how to prove a parallelogram above). Then demonstrate that all the sides are congruent. To do this, you will need to do the distance formula 4 times. After you are done doing the distance formula 4 times, you can write something like this:

“The quadrilateral is a rhombus because it’s a parallelogram with all congruent sides”.

How to prove a quadrilateral is a rectangle

To prove a quadrilateral is a rectangle you must first prove the quadrilateral is a parallelogram (See how to prove a parallelogram). Then demonstrate that the diagonals are congruent. To do this, you will need to do the distance formula 6 times (4 because of the sides and 2 for the diagonals). After you are done doing the distance formula 6 times, you can write something like this:

“The quadrilateral is a rectangle because it’s a parallelogram with congruent diagonals”.

How to prove a quadrilateral is a square

To prove a quadrilateral is a square you must prove that the quadrilateral is a parallelogram, rhombus and a rectangle (See all of the above). To do this, you will need to do the distance formula 6 times (4 because of the sides and 2 for the diagonals). After you are done doing the distance formula 6 times you can write something like this:

“The quadrilateral is a square because it’s a parallelogram with all congruent sides and congruent diagonals”.